Color Painting and the Map Problem (1970)
Artforum, Vol. 8, (March, 1970) pp. 60 - 61.
I
In several essays for this magazine I have written that mutual isolation of pictorial units is a problem for abstract painting. This essay is a further discussion of the negative importance of isolation and an explanation of the "Map Problem," problem of Topology (the mathematics of surface), the effects of which are relevant to abstract painting and the understanding of which will clarify an obstacle inherent in abstract color painting.
I have always assumed as self-evident that the mutual isolation of picture units weakens a painting. It is easy to get agreement to this assumption because it seems right. It has always been my experience that isolated picture units render failed art. But there is no proof of cause. Perhaps there cannot be. To prove it we must specify criteria for art quality, which no one has been able to do. Or we must be content with a reasonable argument.
Painting is relational. "Non-relational" paintings have been made, by painting a canvas all one color, or by leaving it blank. But these works have little esthetic life. They are literal, "idea art," and the idea does not bear much repeating. Paint and canvas have evolved for hundreds of years as part of the process of painting relational paintings and their use for "minimal" expression is simply awkward. The impulse to reduce visible relations finds its natural expression as sculpture, where variety and extreme simplicity can co-exist and harbor "different" styles. To boot, very good painting has always been overtly relational; no really good non-relational painting has been made. This does not mean that art quality arises from the interaction of visible parts, like sparks struck from flint on steel. It is only an indication that art quality as it is found in painting probably cannot come about without visibly related parts.
Pictorial isolation can only exist as a form of pictorial relationship. There can be no notion of isolation if there is no notion of relationship. A painting is presented as a clearly defined unit and requests that we observe what is on its surface. These pictorial units have an automatic, or forced, relationship simply because they are given to us as parts of a clear whole. But they may not interact. If the elements of a picture are not given a proper arena for free interaction they either stand alone or exhaust themselves on their immediate neighbors. Then the painting is only a series of disparate incidents. These incidents coalesce into their own visual wholes and ask to be on their own, perhaps on another canvas. They make another "picture." Thus the wholeness of the picture is fractured, and the structure gives in, like a grocery-store pyramid of tin cans when a bottom can is pulled out.
Interaction is built into most traditional painting because the illusion of deep space allows the painted parts to "reach" one another and because depicted real things are preassembled in the viewer's mind - he does not have to question matters of placement, proportion, color, shading, and so forth, because he sees them as a reflection of real life. Cubism kept an illusion of space in depth and reduced variety of color and form; it is "about" space and is essentially linear. Things are set up in the Cubist painting so that variation and relation of forms carry the painting. Forms are varied by edge and in painting all edge is effectively linear. Indeed, Cubism bloomed into the great linear painting of Jackson Pollock, who took the line and threw out the form it enclosed.
Recently, artists who have been making the very best paintings have been making them in terms of color rather than space. Just as the Cubists reduced color variety these artists often reduce spatial variety, or the importance of spatial variety.
Painting in terms of color brings up special problems of isolation and interaction. Color is an attribute of surface and shows best spread out flat, which declares that the surface occupied is flat. Color painting tends to an elaboration of color, to the use of many colors. Many colors spread at random on a visually flat surface are each isolated from most of the other colors on that surface because each color can interact only with those colors sharing its borders. Thus overall interaction is severely restrained. There are ways around this; I described a few in "Notes on American Painting of the Sixties" (Artforum, January, 1970).
But here I want to point to an interesting fact which, when understood, makes some problems of abstract color painting come clear: no more than four flat opaque color areas can share each other's borders. This means that a fifth color area added to any conglomerate of four other areas must be separate from at least one of these colors. As the number of different colors increases so does the instance of separation. This is why map makers need only four colors to differentiate any group of adjoining countries or states on any flat map. It is a primary obstacle for color painters, who, unlike map makers; want to get their colors together.
In what follows below, I have prepared a common-sense proof of the facts of the Map Problem. Understanding it gives a sense of the difficulty of color painting and may increase appreciation of that type of painting and other painting. By the way, there is no mathematical proof of these facts.1 The Map Problem is a tough nut for topologists and painters alike.
II
The proposition is that no more than four two-dimensional shapes can share each other's borders, compelling isolation of any fifth shape from at least one of the first four.
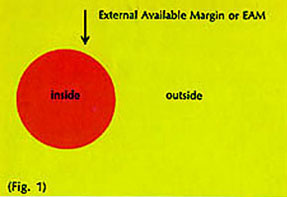
A two-dimensional shape is perfectly flat and is entirely bounded by a margin. It has an inside and an outside. The inside might be defined as that area of a finite shape in which a straight line extended longer than the margin would necessarily strike the margin. The outside is any other area (Fig. 1).

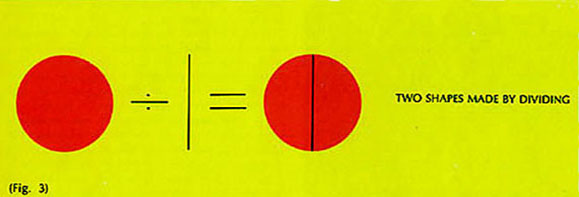

For the sake of the proof we can specify that the creation of a group of two or more shapes must be a process of addition (Fig. 2) rather than division (Fig. 3) because the only difference is priority in time, which is not visible as an effect. Any case of division can be duplicated in terms of addition.
If we rule out division as a means of multiplying shapes we see that the part any shape has to become contiguous with another shape is the external available margin (1), hereafter EAM. Two shapes must share EAMs to be contiguous, by definition. A shape cannot become contiguous to another shape unless both have some EAM to do it with.
There are two cases of contiguity of two shapes:
1. Only one shape has EAM (Fig. 4). This means the other is 100%, surrounded; another shape cannot be added to it. For our purposes we are trying for as much mutual touching as possible so we'd better forget about this.
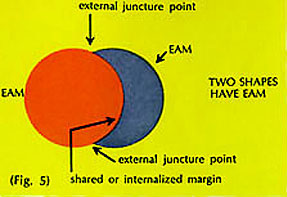
2. Two shapes have EAM (Fig. 5). This is the next step. There are a number of things to take note of before we go on:
a) A shared margin (5), is always internalized because what was once an EAM has become the internal margin of another shape.
b] Any juncture point (5) must be the terminus of at least one internalized margin. There is no juncture if there is no internal margin. Otherwise the EAM would be continuous.
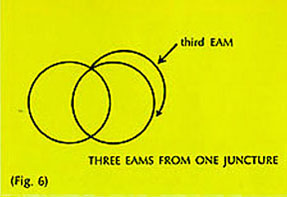
c] No juncture can be the terminus of more than two EAMs. If there were a third EAM (Fig. 6) it would have to come around and attach to one of the other EAMs sooner or later and internalize it.
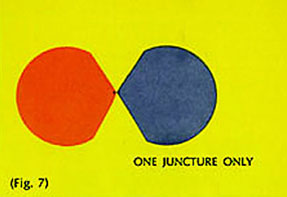
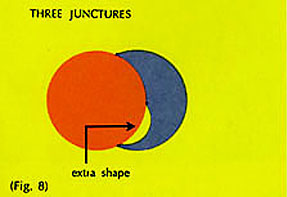
d] Two contiguous shapes can only have two junctures. If there is one juncture (Fig. 7) there is no contiguity. If there are three junctures (Fig. 8) there must be two internalized margins and three shapes.
e] An EAM must terminate on two external junctures (6) because it can only proceed between two external junctures. If its junctures are internalized then the EAM will be.
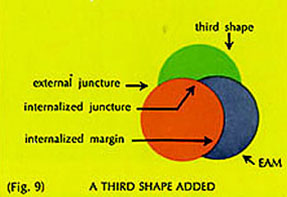
If a third shape is added to the first two (Fig. 9) it must internalize at least one prior juncture, because its touching margin must be contiguous to the first two and continuous. This shape adds two external junctures and takes away one, leaving three. Therefore there can only be three EAMs because each juncture can serve no more than two EAMs, and each juncture shares its EAMs with the other junctures. If each of the three shapes retains an EAM, each EAM between two external junctures must belong to one of the shapes, and they must be continuous, that is, EAM No. 1 - juncture - EAM No. 2, etc.
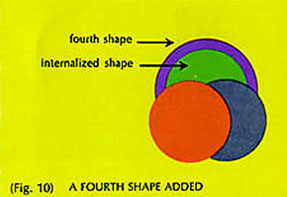
A fourth shape (Fig. 10) added to be contiguous to the first three must have a margin which begins at an external juncture or somewhere along one of the EAMs. This margin must be contiguous with all three prior shapes. The EAMs of these shapes are in sequence, so the margin of the fourth must be continuous along the entire length of one of these EAMs to get from the first to the third, thus internalizing it and its shape. Furthermore, the margin of the fourth shape internalizes two junctures and adds two, so there are four shapes and only three external junctures, enough for only three EAMs.
Therefore the addition of the fourth shape will internalize one of the first three, and a fifth shape added to the four must be isolated from the internalized shape.
This clearly demonstrates that only four flat shapes can have contiguous borders.2
Footnotes
1. As of 1970, when this was written.
2. This last sentence is not part of the article as it appeared in the magazine.
[end]